 |
|
PSSM Intro
(Тут я только рассмотрю карты с направленным источником света (солнце))
Обычные теневые карты имеют множество ограничений. Если вы захотите качественных теней на большом пространстве – вам потребуется большая текстура. Но даже 4096*4096 – не хватит для сцены 1000*1000. Качество будет сильно падать. А если видимость составляет 3000? Просто нереально увеличивать размеры карты – ведь 4к*4к – это уже 64 мегабайта (учитывая 32 битные карты). Что много, а ее все равно не хватит. Что же делают. А делают вот что.
Представим себе главный View Frustum – пирамиду взгляда. Т.е. пирамиду взгляда игрока. Эту пирамиду бьют на части параллельными плоскостями (все они параллельны плоскостям отсечения главного фрустума) – получая при этом несколько фрустумов. Отсюда и происходит название PSSM.
Отобразим схематично.
Вот наш главный фрустум и сцена, вид сбоку.
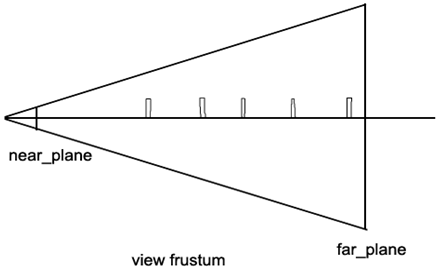
Рис.1. Схема пирамиды вида – Фрустума.
Сам фрустум далее разбивается параллельными плоскостями – далее по тексту – сплитами.
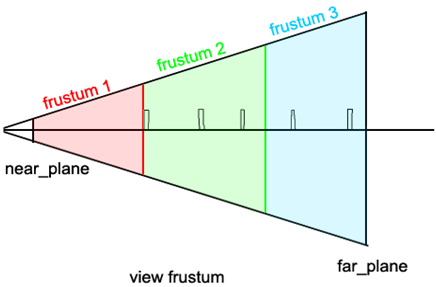
Рис.2. Схема разбиения пирамиды вида, на несколько, параллельными плоскостями.
Для каждого фрустума строятся свои матрицы View и Proj для источника света. Вот основная проблема у меня была понять как они строятся. Но это позади.
Для начала реализации PSSM мы определяем новую структуру, которая полностью опишет каждый фрустум
struct frustum
{
float neard; //ближняя плоскость отсечения
float fard; //дальняя плоскость отсечения
float fov; //угол обзора
float ratio; // ширина/высоту кадра (1,333)
D3DXVECTOR3 point[8]; //восемь точек пирамиды фрустума в мировых координатах
D3DXVECTOR3 center; //центр фруструма в мировых координатах
};
//будет три сплита
frustum f[3];
float split_weight=0.95f; //коэффициент разбиения, подбирается вручную. |
Перво наперво мы определяем на сколько удалены плоскости от центра камеры. Для этого используют простое разбиение фрустума :
// updateSplitDist считает ближнию и дальнию дистанцию для каждого разреза фруструма
// в камера спейсе - это так, дистанция начала и конца слайса
void updateSplitDist(frustum f[3], float nd, float fd)
{
float lambda = split_weight;
float ratio = fd/nd; //fn=0.25, fd=FAR_DIST=3000.0f; //все от непорезаного фруструма
f[0].neard = nd; //у ближнего сплита, ближняя плоскость = ближней плоскости непорезаного фруструма...
for(int i=1; i<3; i++)
{
float si = i / (float)3;
f[i].neard = lambda*(nd*powf(ratio, si)) + (1-lambda)*(nd + (fd - nd)*si);
f[i-1].fard = f[i].neard * 1.005f;
}
f[3-1].fard = fd;//у дальнего, дальняя плоскость = дальней непорезаного фрустурма
} |
Поясню. На вход мы даем только nd - ближнюю плоскость отсечения, и fd – дальнюю плоскость отсечения. На выходе мы получаем заполненные поля (fard,neard) наших фрустумов
К примеру – основная матрица проекции в программе задана так :
// Инициализируем проекционную матрицу
D3DXMatrixPerspectiveFovLH( &mProj, ( float )D3DX_PI / 4, ((float)wWidth/(float)wHeight), 0.25f, 3000.0f ); |
Как видим ближняя плоскость равна 0,25 а дальняя 3000.
Главная ошибка новичков – это установка ближней плоскости в 0. Этого делать категорически нельзя – иначе будут ошибки. Т.к. при расчете будет попытка деления на 0.
Поэтому перед рендером теней, сразу же вызываем расчет дистанций
updateSplitDist(f, 0.25f, 3000.0f); //получим f.farn, и f.fard каждого сплита... |
Т.к. у нас будет три теневых карты, в шейдере при наложении теней мы должны понять, где заканчивается один сплит и начинается другой. Для этого мы рассчитываем так называемые Зед-боунд – просто границы сплитов.
Рассчитываются довольно просто :
D3DXVECTOR4 far_bound;
D3DXVECTOR4 bound;
float far_b[3];
for (int i=0; i<3; i++)
{
D3DXVec4Transform(&bound,& D3DXVECTOR4(0,0,f[i].fard,1),&mProj); //на главную проекцию
far_b[i]=bound.z;
}
//Вектор для сравнения в шейдере позиции точки, - определение сплита для участка
far_bound = D3DXVECTOR4(far_b[0],far_b[1],far_b[2],1); |
Для нашего примера, я получил такие значения fard :
Для первого сплита – 55,72
Для второго сплита – 225,61
Для третьего сплита – 3000,0
После применения проекции значения стали такими (вектор far_bound ) :
Для первого сплита – 55,47
Для второго сплита – 225,38
Для третьего сплита – 3000,0
Этот вектор после передачи в шейдер мы сравниваем с позицией точки (уже умноженной на видовую и проекционную матрицу)
Вот так это выглядит у меня (пиксельный шейдер):
SliceCol[0]=float4(1,0,0,1);
SliceCol[1]=float4(0,1,0,1);
SliceCol[2]=float4(0,0,1,1);
float4 SCOLOR=0.1;
int index=0;
if(input.Pos.z*input.Pos.w < far_d.x)
{SCOLOR = SliceCol[0];index=0;}
else if(input.Pos.z*input.Pos.w < far_d.y)
{SCOLOR = SliceCol[1];index=1;}
else if(input.Pos.z*input.Pos.w < far_d.z)
{SCOLOR = SliceCol[2];index=2;}
return col+SCOLOR/2; |
Умножением Z*W – я отменяю проецирование точки – возвращая ее реальные координаты z (не гомогенные)
При этом сцена раскрашена так :

Ближний сплит – красный, средний зеленый, дальний синий.
Вторая процедура, которую нужно одолеть – это расчет всех точек каждого фрустума. Поясню. Каждый фрустум, (как мы можем видеть на рисунке 2.) – является усеченной пирамидой. Т.е. содержит 8 точек, которыми можно ее полностью описать. Их-то мы и найдем. Также мы найдем центр фрустума.
Для этого нам понадобятся мировая позиция камеры, и вектор направление взгляда.
Кто пользуется собственными или сторонними классами камер – тем легче, остальным показываю как извлечь нужные вектора из матрицы вида.
D3DXMATRIX invView;
D3DXMatrixInverse(&invView,NULL,&mView); //mView – матрица вида
D3DXVECTOR4 cam_pos=D3DXVECTOR4(invView._41,invView._42,invView._43,invView._44);
D3DXVECTOR3 view_dir = D3DXVECTOR3(mView._13,mView._23,mView._33);
//Также заполним дополнительные параметры наших фрустумов
f[0].fov = (float)D3DX_PI / 4 ;
f[0].ratio = (float)wWidth/(float)wHeight;
f[1].fov = (float)D3DX_PI / 4 ;
f[1].ratio = (float)wWidth/(float)wHeight;
f[2].fov = (float)D3DX_PI / 4 ;
f[2].ratio = (float)wWidth/(float)wHeight; |
wWidth/ wHeight – разрешение экрана. В даном примере 1024*768. Угол обзора стандартный – 45 градусов.
Ниже привожу функцию которая расчитывает позиции вершин фрустума в мировых координатах, и центра фрустума. На вход идет center (позиция камеры), и view_dir – направление взгляда. Функция взята из примера №1 (сайта nVidia, про пальмы)
void updateFrustumPoints(frustum &f, D3DXVECTOR3 ¢er, D3DXVECTOR3 &view_dir)
{
D3DXVECTOR3 up(0.0f, 1.0f, 0.0f);
D3DXVECTOR3 right;
D3DXVec3Cross(&right,&view_dir,&up);
D3DXVECTOR3 fc = center + view_dir*f.fard;
D3DXVECTOR3 nc = center + view_dir*f.neard;
D3DXVec3Normalize(&right,&right);
D3DXVECTOR3 tmp;
D3DXVec3Cross(&tmp,&right,&view_dir);
D3DXVec3Normalize(&up,&tmp);
// тут высота и ширина являются половиной высот ширины of
// ближнего и дальнего прямоугольника плоскости отсечений
float near_height = tan(f.fov/2.0f) * f.neard;
float near_width = near_height * f.ratio;
float far_height = tan(f.fov/2.0f) * f.fard;
float far_width = far_height * f.ratio;
f.point[0] = nc - up*near_height - right*near_width;
f.point[1] = nc + up*near_height - right*near_width;
f.point[2] = nc + up*near_height + right*near_width;
f.point[3] = nc - up*near_height + right*near_width;
f.point[4] = fc - up*far_height - right*far_width;
f.point[5] = fc + up*far_height - right*far_width;
f.point[6] = fc + up*far_height + right*far_width;
f.point[7] = fc - up*far_height + right*far_width;
D3DXVECTOR3 vCenter(0,0,0);
for (int i = 0; i < 8; i++)
vCenter += f.point[i];
vCenter /= 8;
f.center = vCenter;
} |
Для проверки правильности наших действий – сильно рекомендую загрузить модели (к примеру простейшая сфера с радиусом 1) – и разместить ее в центре первого сплита, потом второго и третьего. Также разместить сферы для каждого сплита в последних четырех вершинах (с 4 до 8 вершины) Должн выглядеть примерно так :

Как видим все в норме =) Центр фрустума – шар входит в землю идеально в центре красного сплита. Также видны угловые сферы. Если опускать камеру вниз – они должны входить в землю – на границе красного и зеленого сплита.
Если у вас всё также – Вы на верном пути. Это значит все точки сплита рассчитаны верно.
<< Назад | Следующая страница >>
|
Copyright CSS PSV 2009 Kherson
|
|
